There are a lot of fun theories out there, and the simulation hypothesis is one of them. As usual, Wikipedia puts it best:
The simulation hypothesis or simulation theory proposes that all of reality, including the Earth and the universe, is in fact an artificial simulation, most likely a computer simulation.
The idea that our universe might simply be a computer program running on an alien’s Raspberry Pi is fun to entertain, but most of us don’t take the idea seriously. It’s a thought experiment, if anything.

However, there are people out there who decided to take the idea to its limits. Some physicists raised over $200,000 in an effort to conduct some experiments based on the assumption; they even published a paper on their results (not very compelling). It’s strange to think it’s possible to determine whether or not you’re in a simulation while abiding by its rules, but this is exactly the topic of George Hotz’ talk on “hacking” our way out of the simulation.1
So where am I going with this?
Well, IF we continue to operate under the premise that our world is an accurate simulation of a larger world (and that’s quite a big “if”), then it’s possible that our collective feeling of increasingly-unsettling uncertainty in the world is caused by the fact that we’re reaching the hardware limitations of the computer our simulation is running on.
On Minecraft
The voxel-based survival simulator Minecraft that jolted the indie game industry into overdrive is, weirdly enough, the inspiration for my reasoning. Minecraft is a procedurally-generated game, meaning everything from the shape of the trees to the mineral deposits hidden deep within caves is randomly generated. It’s the result of a mathematical process involving Perlin noise which is at the core of many games that generate content as the user explores.
Because this process, the world is essentially infinite: you can go as far as you want in any given direction and there will always be something fresh and exciting waiting for you. Of course, “infinity” can’t actually exist on a computer: for example, an Int32 type can only store ~4 billion numbers, so if you’re using one to store the 3D positional coordinates of a player, they can’t go more than 2 billion steps from their starting point along a particular axis.
Obviously, 2 billion steps is still huge, so players don’t ever naturally encounter these limits. Minecraft stays effectively infinite, but that does not mean the world is without problems. Players of the game may already be aware of the Far Lands: the oddities that occur when you reach these “edges” of the generated world. Things start to look really strange when you get there:
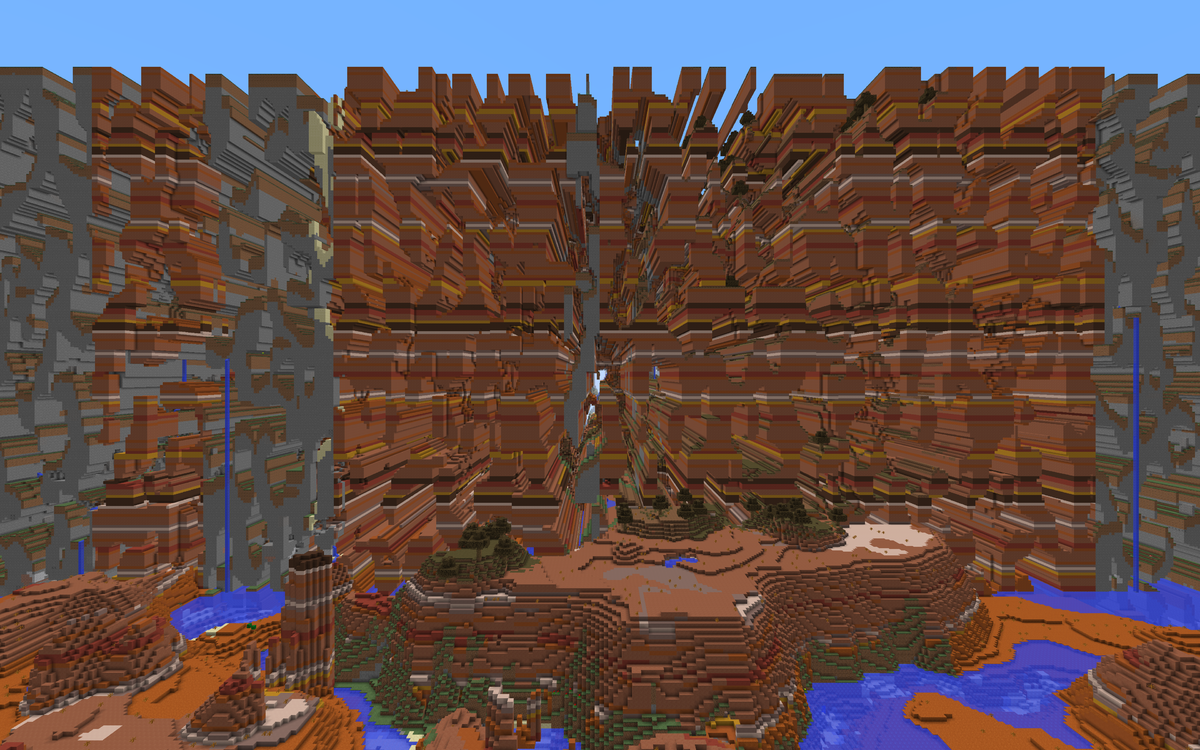
A view of the Minecraft’s Far Lands.
This erratic-yet-structured pattern of blocks is a result of the terrain-generating algorithm going haywire. Fundamentally, it’s a result of floating point imprecision which is a natural, unavoidable limitation of modern computer hardware.
On Floating Point
Without getting too technical, it’s worth quickly explaining how decimal numbers work on a computer. At the end of the day, bits are bits, and decimal numbers are simply a human-defined way of interpreting those bits. To drive this home, the following 32 bits can be interpreted as the decimal 123456.789, the number 1206984820, or even as the nonsensical string Gñ e:
$$
01000111 \; 11110001 \; 00100000 \; 01100101
$$
We (as in, the collective “we” of computer scientists) have agreed to interpret bits as decimals using the IEEE-754 standard, which essentially specifies that a certain number of bits is the exponent while the rest are the actual value.2 The decimal or “floating point” type is supposed to be able to represent values from $2^{-127}$ to $2^{127}$.
For example the decimal above is actually interpreted in three chunks: $$ \underbrace{ 0 }_{\text{sign}} \underbrace{ 10001111 }_{\text{exponent}} \; \underbrace{ 11100010 \; 01000000 \; 1100101 }_\text{mantissa} $$
The exponent is interpreted as 16 while the mantissa is interpreted as 1.8838011026382446. Then, the final value is just their product; for our specific bits, this comes out to $$ 2^{16} \times 1.8838011026382446 = 123456.789063 $$
Hold on, didn’t we want exactly 123456.789? Yup, but we instead got a value that was 0.000063 larger. Therein lies the rub: computers can’t store decimals exactly, and the error gets worse as the numbers get larger. For example, if we instead wanted to represent the decimal 123456789.123456789, the best a computer could do is 123456792! That’s off by ~2.87… pretty significant.
This behavior is the cause of the Far Lands above: the terrain generating starts behaving strangely because it can’t properly interpolate between large decimal values as your $(x,y,z)$ position in the world grows.
Our Simulation
It’s hard to truly put a finger on what’s out of the ordinary. Perhaps it’s that the U.S. has a TV star as a president; regardless of your political stance, this is weird. Maybe it’s the increased severity in natural disasters: earthquakes, fires, and viruses all feel more common than they used to, and let’s hope we don’t see another Big One in our lifetimes. It could just be the whacky weather patterns, like certain places seeing snow in May or heat records being broken seemingly every year.
It just seems like we’re on the brink of something… Regardless of the root cause, I think you know the feeling I’m talking about.
If we really do live in a simulation, the ever-increasing oddities could be explained by the fact that we’re reaching the limits of the hardware that powers it, just like the limitations of floating points created the Far Lands in Minecraft. Naturally, if such a hypothesis were to hold true, we should be able to observe things get weirder and weirder as time goes on. With the direction the political, economic and literal climates are trending, that seems likely. Under this theory, though, we might even see a law of physics break; wouldn’t that be something?
For now, I’ll try to find solace in the idea that our simulation must soon be coming to an end.