Introduction

In an decentralized network, not every user is aware of every other. In the case of Cicada, for example, a packet may hop through many users before reaching its destination. How, then, does a user ensure that its broadcast message is received by everyone?

Solution 1: The Shotgun Approach

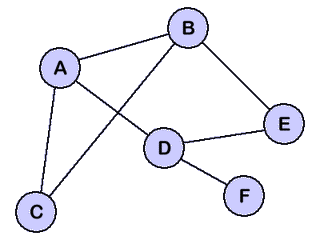
Suppose a pretty simple network oriented like the one above. Clearly, not every node is directly connected to every other. How does node $C$ ensure that node $D$ receives an arbitrary message?

The simplest approach is very straightforward:

When a node receives a broadcast message, it sends it to everyone it’s connected to, except for whomever it received the message from. This guarantees that every node will receive the message, but comes with a host of problems. Notice the amount of duplicate messages this will generate! A node like $B$ will still get two copies of the data (from $A$ and from $C$). Furthermore, how do we know when to “stop” broadcasting? In the network, there is a cycle of $C \rightarrow A \rightarrow B \rightarrow C$ that will infinitely “broadcast.”

Caching Broadcasts

To solve the loop problem, nodes could simply track the messages they’ve seen. If a node has seen a message, it doesn’t re-broadcast. This, unfortunately, opens up the network to a [distributed] denial-of-service attack! A user can endlessly spam massive broadcast messages to hog all of the storage space on the nodes! Even if we store unique hashes of messages (which would usually be smaller than the message content), the problem remains; it just requires more messages.

We need another option. The solution should have minimal message duplication as well as no node memory usage.

Analysis

Even with caching, how much message duplication will there be in our simple sample network? Well:

• $C$ sends to ${ A, B }$.
• $A$ sends to ${ B, D }$ (duplicates = 1).
• $B$ sends to ${ A, E }$ (duplicates = 2). Remember, even though $A$ sent to $B$ above, this likely happened after $B$ already got the message from $C$, so the “return to sender” optimization doesn’t apply.
• $E$ sends to $D$ (duplicates = 3).
• $D$ sends to ${ F, E }$ (duplicates = 4).

This value highly varies depending on the network structure, and the “connectivity” of the network graph.

Solution 2: Packet Caching

We can solve both of these problems in one go by using the message itself for memory. Inside of the message, we store a fixed-size stack of the nodes that this broadcast message has visited thus far. Once the stack reaches its maximum limit, the oldest nodes are removed to make way for the new ones. This means that messages always contain more relevant information based on the location of the message itself! Obviously, the bigger this stack, the less duplication will occur.

Formally, we could have a message format like this: $$ \begin{aligned} &D, &\small\text{the size of the stack} \\ &I_1, &\small\text{oldest visited node} \\ &I_2, &\small\text{next oldest visited node} \\ &I_3, &\small\text{and so on}\ldots \\ &L, &\small\text{the message length} \\ &M &\small\text{the actual message} \\ \end{aligned} $$

Analysis

Here’s the sample network again:

Let’s analyze the number of duplicates this generates. Suppose we choose a “stack size” of $\lceil{\log_2{n}}\rceil = 3$, where $n$ is the number of nodes:

• $C$ sends to $A$ and $B$, the stack is ${ A, B }$.
• $A$ re-broadcasts to $D$ and $B$ re-broadcasts to $E$, adding each of these to the stack, respectively.
• $D$ sends to $E$ (first duplicate!), setting the stack to ${ B, E, F }$.
• $E$ sends to $D$ (from $B$’s message, not from the above message); the stack is ${ A, B, D }$ and this is the 2nd duplicate.
• Finally, $F$ gets the message and does nothing.

Thus, we only got 2 duplicates in the network at absolutely no memory cost to each node. Furthermore, in a more intelligent network nodes might be more aware of their direct neighbors and have even less duplication! For example, if $B$ sees a stack of ${ A, B }$ and knows that there’s an edge between $A \longleftrightarrow D$, it could preemptively set the stack to be ${ A, D, E }$, eliminating all possible duplicates!

Conclusion

Even for the small sample network, we cut the amount of duplicates in half; furthermore, none of the nodes need to store anything in memory. We’ve achieved the two goals we were looking for in the beginning! I use this technique in Cicada for broadcast packets.¹ It can actually be further optimized since each node in a Cicada swarm knows a few details (like immediate neighbors) about a handful of other nodes in the network.

This kind of optimal broadcasting can be extremely important in a P2P content distribution platform. For example, in a live-streaming network in which a single user broadcasts their data to the rest of the swarm, this minimizes the strain on the content broadcaster as well as on the viewers.²